We always want more information. So, understanding complex machine learning models is an ongoing challenge to people like us. Among the various methodologies developed to explain a model’s decisions, Shapley Values stand out due to their robust theoretical foundation and increasing practical applications. So, if you haven’t heard of it, consider subscribing to my Substack to learn more.
What are Shapley Values?
Shapley Values have their roots in cooperative game theory, introduced by Lloyd Shapley. Their primary function is to fairly distribute rewards among players in a cooperative game based on their contribution. When applied to machine learning, Shapley Values measure the contribution of each feature to a particular prediction, offering a deeper insight into the model’s decision-making process.
To illustrate, consider the following scenario:
Imagine you’re coordinating a strategic defence mission. This mission involves various specialised units: intelligence operatives gathering crucial info, drone pilots conducting aerial surveillance, ground troops ensuring territorial security, and a tech team jamming enemy communications.
At the mission’s conclusion (assuming it was a success) how would you attribute the mission’s success? Was it the timely intelligence gathered, the strategic aerial oversight, the resilience of the ground troops, or the tech disruption that did its job? Is there a way to evaluate each part’s contribution so you can improve or replicate in a new mission?
This scenario mirrors the dynamics in machine learning. Each model can be viewed as a mission, where the distinct features are analogous to the specialised units contributing to the mission’s outcome—most of our models are not even close to a 007 scenario, but you get the idea. Some features (‘units’) might heavily influence the model’s decision, whilst others play a supporting or minor role. The “success” of this mission is equivalent to how well the model predicts, relative to a given baseline.
Shapley Values provide a means to fairly distribute the “commendation” for the model’s success amongst its features. This ensures that every feature’s contribution is evaluated, considering all the possible collaborations and interactions that could occur between them.
The mathematical essence behind Shapley Values remains rooted in cooperative game theory. The formulation involves evaluating all possible combinations of features. The Shapley formula ensures that each feature's contribution is assessed equitably, accounting for all potential coalitions or combinations of features.
Relevance in Machine Learning
In machine learning models, particularly those with numerous features, it is vital to understand which features significantly influence predictions. Shapley Values present a systematic approach to gauge the importance of each feature both at the global and local level whilst ensuring the model’s interpretability is not compromised.
Okay, but how does it compare to a standard feature importance technique?
How to Utilise Shapley Values?
Given their significance in model interpretation, there are some libraries to facilitate the computation of Shapley Values for machine learning models. I use SHAP (SHapley Additive exPlanations). This Python library allows us to obtain Shapley-based explanations for predictions made by a wide variety of models.
While I don’t like toy datasets, they are helpful to explain concepts in situations like these. So, consider a simple example where we use a Random Forest classifier on the Iris dataset and then evaluate the influence of features using Shapley Values.
import shap ## you might have to pip install shap
from sklearn import datasets
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
# Load dataset
df = datasets.load_iris()
X = df.data
y = df.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# Train the model
model = RandomForestClassifier()
model.fit(X_train, y_train)
# Using SHAP to explain predictions
explainer = shap.Explainer(model)
shap_values = explainer(X_test)
# Visualising the Shapley Values for the second class (e.g., virginica)
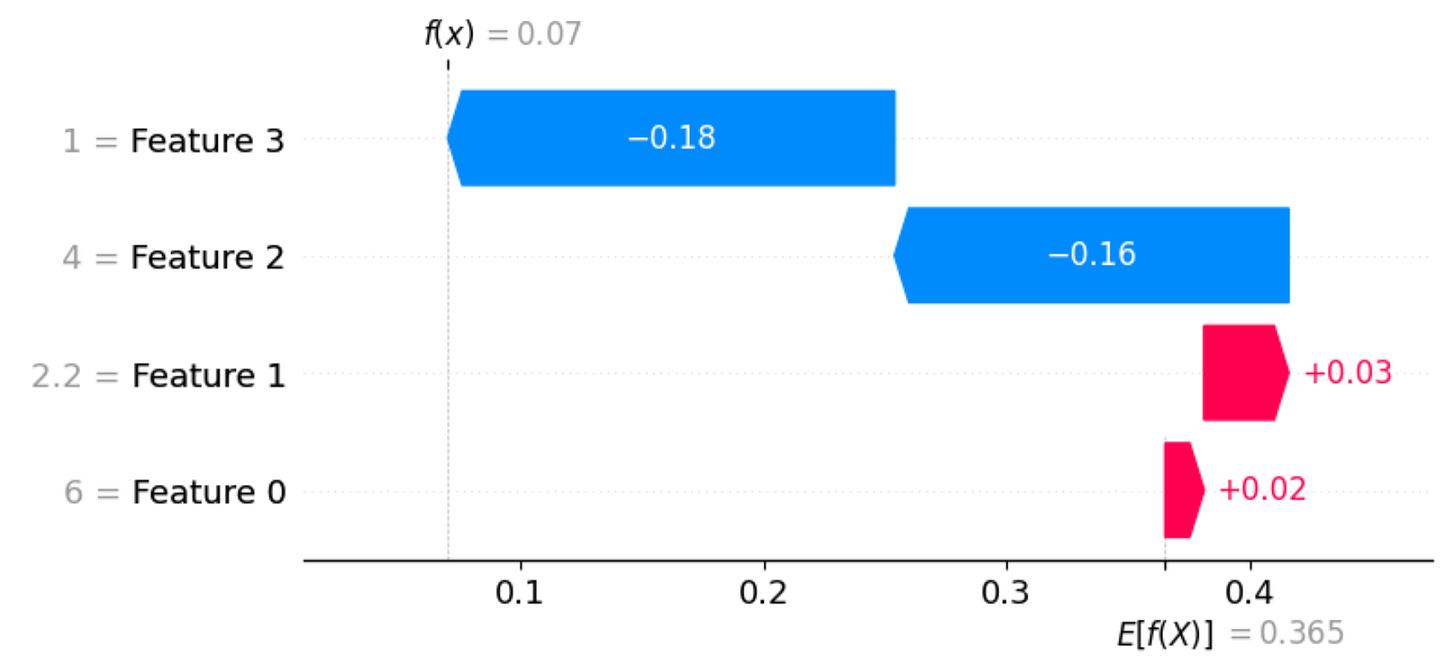
shap.plots.waterfall(shap_values[1,:,2])If you run the code above on your IDE, then you should get the following plot:
To give a more contextual interpretation:
The sepal length of 6.0 cm and sepal width of 2.2 cm for this instance slightly push the model towards classifying it as virginica.
However, the petal length of 4.0 cm and petal width of 1.0 cm pull the model away from classifying it as virginica, and they have a stronger negative influence than the positive influence of the sepal dimensions.
This kind of interpretation allows you to understand how each feature contributes (positively or negatively) to the model’s prediction for this specific instance.
(Honest) Conclusion
Shapley Values derived from cooperative game theory and provide a detailed breakdown of feature contributions in machine learning models. However, choosing Shapley Values over traditional feature importance methods isn’t necessarily ‘better’, it depends on your specific needs. For a quick overview (which usually is what we need to get things done), traditional methods are okay; but, for detailed insights into feature interactions, Shapley Values are an excellent alternative. If you have time to use both, then— besides being lucky— you can get a comprehensive understanding of your model’s behaviour.